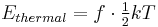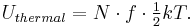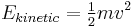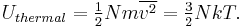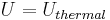Thermal energy
Thermal energy is the part of the total internal energy of a thermodynamic system or sample of matter that results in the system's temperature. The internal energy, also often called the thermodynamic energy, includes other forms of energy in a thermodynamic system in addition to thermal energy, namely forms of potential energy, such as the chemical energy stored in its molecular structure and electronic configuration, intermolecular interactions, and the nuclear energy that binds the sub-atomic particles of matter.
Microscopically, the thermal energy is the kinetic energy of a system's constituent particles, which may be atoms, molecules, electrons, or particles in plasmas. It originates from the individually random, or disordered, motion of particles in a large ensemble. The thermal energy is equally partitioned between all available quadratic degrees of freedom of the particles. These degrees of freedom may include pure translational motion in fluids, normal modes of vibrations, such as intermolecular vibrations or crystal lattice vibrations, or rotational states. In general, the availability of any such degrees of freedom is a function of the energy in the system, and therefore depends on the temperature.
When two thermodynamic systems with different temperatures are brought into diathermic contact, they exchange energy in form of heat, which is a transfer of thermal energy from the system of higher temperature to the colder system. This heat may cause work to be performed on each system, for example, in form of volume or pressure changes. This work may be used in heat engines to convert thermal energy into mechanical energy. When two systems have reached a thermodynamic equilibrium, they have attained the same temperature and the net exchange of thermal energy ceases.
Thermal energy is distinct from heat. In the strict use in physics, heat is a characteristic only of a process, i.e., it is absorbed or produced as an energy exchange, but it is not a static property of matter. Matter does not contain heat, but thermal energy. Heat is thermal energy in the process of transfer or conversion across a boundary of one region of matter to another.[1]
Contents |
Definitions
Thermal energy is the portion of the internal energy that is responsible for a system's temperature. Microscopically, the thermal energy is identified with mechanical kinetic energy of the constituent particles or other forms of kinetic energy associated with quantum-mechanical microstates. The distinguishing difference between the terms kinetic energy and thermal energy is that thermal energy is the mean energy of disordered, i.e., random, motion of the particles or the oscillations in the system. The conversion of energy of ordered motion to thermal energy results from collisions.[2]
All kinetic energy is partitioned into the degrees of freedom of the system. The average energy of a single particle with f quadratic degrees of freedom in a thermal bath of temperature T is a statistical mean energy given by the equipartition theorem as
where k is the Boltzmann constant. The total thermal energy of a sample of matter or a thermodynamic system is consequently the average sum of the kinetic energies of all particles in the system. Thus, for a system of N particles its thermal energy is[3]
In general, however, Uthermal is not the total energy of a system. Physical systems also contains static potential energy (such as chemical energy) that arises from interactions between particles, nuclear energy associated with atomic nuclei of particles, and even the rest mass energy due to the equivalence of energy and mass.
Historical context
In a 1847 lecture entitled On Matter, Living Force, and Heat, James Prescott Joule characterized the terms latent heat and sensible heat as components of heat each effecting distinct physical phenomena, namely the potential and kinetic energy of particles, respectively.[4] He describes latent energy as the energy of interaction in a given configuration of particles, i.e., a form of potential energy, and the sensible heat as an energy affecting the thermal energy, which he called the living force.
Thermal energy of the ideal gas
Thermal energy is most easily defined in the context of the ideal gas, which is well approximated by a monatomic gas at low pressure. The ideal gas is a gas of particles considered as point objects of perfect spherical symmetry that interact only by elastic collisions and fill a volume such that their mean free path between collisions is much larger than their diameter.
The mechanical kinetic energy of a single particle is
where m is the particle's mass and v is its velocity. The thermal energy of the gas sample consisting of N atoms is given by the sum of these energies, assuming no losses to the container or the environment:
where the line over the velocity term indicates that the average value is calculated over the entire ensemble. The total thermal energy of the sample is proportional to the macroscopic temperature by a constant factor accounting for the three translational degrees of freedom of each particle and the Boltzmann constant, converting units between the microscopic model and the macroscopic temperature. This formalism is the basic assumption that directly yields the ideal gas law, and it shows that for the ideal gas, the internal energy consists only of its thermal energy:
Distinction of thermal energy and heat
In engineering and technology, and particularly in fields that deal with civil energy use and conservation in building construction, heating systems, and power generation, heat and thermal energy are often indiscriminately used interchangeably.
In thermodynamics, heat must always be defined as energy in exchange between two systems, or a single system and its surroundings.[5] According to the zeroth law of thermodynamics, heat is exchanged between thermodynamic systems in thermal contact only if their temperatures are different. For the purpose of distinction, a system is defined to be enclosed by a well-characterized boundary. If heat traverses the boundary in direction into the system, the internal energy change is considered to be a positive quantity, while exiting the system, it is negative. Heat is never a property of the system, nor is it contained within the boundary of the system.
In contrast to heat, thermal energy exists on both sides of a boundary. It is the statistical mean of the microscopic fluctuations of the kinetic energy of the systems' particles, and it is the source and the effect of the transfer of heat across a system boundary. Statistically, thermal energy is always exchanged between systems, even when the temperatures on both sides is the same, i.e. the systems are in thermal equilibrium. However, at equilibrium, the net exchange of thermal energy is zero, and therefore there is no heat.
Thermal energy may be increased in a system by other means than heat, for example when mechanical or electrical work is performed on the system. No qualitative difference exists between the thermal energy added by other means. There is also no need in classical thermodynamics to characterize the thermal energy in terms of atomic or molecular behavior. A change in thermal energy induced in a system is the product of the change in entropy and the temperature of the system.
Heat exchanged with a system may cause changes other than a change in thermal energy. For example, it may cause phase transitions, such as melting or evaporation, which are changes in the configuration of a material. Since such an energy exchange is not observable by a change in temperature, it is called a latent heat and represents a change in the potential energy of the system.
Rather than being itself the thermal energy involved in a transfer, heat is sometimes also understood as the process of transfer, i.e., it functions as a verb.
Thermal energy of individual particles
The term thermal energy is also often used as a property of single particles to designate the kinetic energy of the particles. An example is the description of thermal neutrons having a certain thermal energy, which means that the kinetic energy of the particle is equivalent to the temperature of its surroundings.
See also
References
- ^ Robert F. Speyer (1994). Thermal analysis of materials. CRC Press. p. 2. ISBN 9780824789633. http://books.google.com/books?id=5vTPIN_Y_FMC&pg=PA2.
- ^ S. Blundell, K. Blundell (2006). Concepts in Thermal Physics. Oxford University Press. p. 366. ISBN 0-19-856769-3.
- ^ D.V. Schroeder (1999). An Introduction to Thermal Physics. Addison-Wesley. p. 15. ISBN 0-201-38027-7.
- ^ J. P. Joule (1884), The Scientific Paper of James Prescott Joule, The Physical Society of London, p. 274, "I am inclined to believe that both of these hypotheses will be found to hold good,—that in some instances, particularly in the case of sensible heat, or such as is indicated by the thermometer, heat will be found to consist in the living force of the particles of the bodies in which it is induced; whilst in others, particularly in the case of latent heat, the phenomena are produced by the separation of particle from particle, so as to cause them to attract one another through a greater space.", Lecture on Matter, Living Force, and Heat. May 5 and 12, 1847
- ^ Thomas W. Leland, Jr., G. A. Mansoori, ed., Basic Principles of Classical and Statistical Thermodynamics
External links
|
||||||||||||||